Linear algebra
Experimental html version of downloadable textbook, see https://theartofhpc.com
#1_1
vdots
#1_{#2-1} \end{pmatrix}} % {
left(
begin{array}{c} #1_0
#1_1
vdots
#1_{#2-1}
end{array}
right) } \] 13.1 : Norms
13.1.1 : Vector norms
13.1.2 : Matrix norms
13.2 : Gram-Schmidt orthogonalization
13.3 : The power method
13.4 : Nonnegative matrices; Perron vectors
13.5 : The Gershgorin theorem
13.6 : Householder reflectors
Back to Table of Contents
13 Linear algebra
In this course it is assumed that you know what a matrix and a vector are, simple algorithms such as how to multiply them, and some properties such as invertibility of a matrix. This appendix introduces some concepts and theorems that are not typically part of a first course in linear algebra.
13.1 Norms
A norm is a way to generalize the concept of absolute value to multi-dimensional objects such as vectors and matrices. There are many ways of defining a norm, and there is theory of how different norms relate. Here we only give the basic concepts.
13.1.1 Vector norms
crumb trail: > norms > Norms > Vector norms
A norm is any function $n(\cdot)$ on a vector space $V$ with the following properties:
-
$n(x)\geq0$ for all $x\in V$ and $n(x)=0$ only for $x=0$,
-
$n(\lambda x)=|\lambda|n(x)$ for all $x\in V$ and $\lambda\in\bbR$.
-
$n(x+y)\leq n(x)+n(y)$
-
The 1-norm
$\|\cdot\|_1$ is the sum of absolute values:
\begin{equation} \| x\|_1 = \sum |x_i|. \end{equation}
-
The 2-norm $\|\cdot\|_2$ is the root of the sum of squares:
\begin{equation} \| x\|_2 = \sqrt{ \sum x^2}. \end{equation}
-
The infinity-norm $\|\cdot\|_\infty$ norm is defined as $\lim_{p\rightarrow\infty}\|\cdot\|_p$, and it is not hard to see that this equals
\begin{equation} \|x\|_\infty=\max_i |x_i|. \end{equation}
13.1.2 Matrix norms
crumb trail: > norms > Norms > Matrix norms
By considering a matrix of size $n$ as a vector of length $n^2$, we can define the Frobenius matrix norm: \begin{equation} \|A\|_F=\sqrt{\sum_{i,j}|a_{ij}|^2}. \end{equation} norms}: \begin{equation} \|A\|_p=\sup_{\|x\|_p=1}\|Ax\|_p= \sup_x\frac{\|Ax\|_p}{\|x\|_p}. \end{equation} From their definition, it then follows that \begin{equation} \|Ax\|\leq\|A\|\|x\| \end{equation} for associated norms.
The following are easy to derive:
-
$\|A\|_1=\max_j\sum_i|a_{ij}|$, the maximum column-absolute sum;
-
$\|A\|_\infty=\max_i\sum_j|a_{ij}|$, the maximum row-absolute sum.
The matrix condition number is defined as \begin{equation} \kappa(A)=\|A\|\,\|A\inv\|. \end{equation} In the symmetric case, and using the 2-norm, this is the ratio between the largest and smallest eigenvalue ; in general, it is the ratio between the largest and smallest singular value .
13.2 Gram-Schmidt orthogonalization
crumb trail: > norms > Gram-Schmidt orthogonalization
The GS algorithm takes a series of vectors and inductively orthogonalizes them. This can be used to turn an arbitrary basis of a vector space into an orthogonal basis; it can also be viewed as transforming a matrix $A$ into one with orthogonal columns. If $Q$ has orthogonal columns, $Q^tQ$ is diagonal, which is often a convenient property to have.
The basic principle of the GS algorithm can be demonstrated with two vectors $u,v$. Suppose we want a vector $v'$ so that $u,v$ spans the same space as $u,v'$, but $v'\perp u$. For this we let \begin{equation} v'\leftarrow v-\frac{u^tv}{u^tu}u. \end{equation} It is easy to see that this satisfies the requirements.
Suppose we have an set of vectors $u_1,\ldots,u_n$ that we want to orthogonalize. We do this by successive applications of the above transformation:
For $i=1,\ldots,n$:
For $j=1,\ldots i-1$:
let $c_{ji}=u_j^tu_i/u_j^tu_j$
For $i=1,\ldots,n$:
update $u_i\leftarrow u_i-u_jc_{ji}$
Often the vector $v$ in the algorithm above is normalized; this adds a line
$u_i\leftarrow u_i/\|u_i\|$
to the algorithm. GS orthogonalization with this normalization, applied to the columns of a matrix, is also known as the QR factorization .
Exercise
Suppose that we apply the
GS
algorithm to the columns of a
rectangular matrix $A$, giving a matrix $Q$. Prove that there is an
upper triangular matrix $R$ such that $A=QR$. (Hint: look at the
$c_{ji}$ coefficients above.) If we normalize the
orthogonal vector in the algorithm above, $Q$ has the additional property
that $Q^tQ=I$. Prove this too.
End of exercise
The GS algorithm as given above computes the desired result, but only in exact arithmetic. A computer implementation can be quite inaccurate if the angle between $v$ and one of the $u_i$ is small. In that case, the MGS algorithm will perform better:
For $i=1,\ldots,n$:
For $j=1,\ldots i-1$:
let $c_{ji}=u_j^tu_i/u_j^tu_j$
update $u_i\leftarrow u_i-u_jc_{ji}$
To contrast it with MGS , the original GS algorithm is also known as CGS .
As an illustration of the difference between the two methods, consider the matrix \begin{equation} A= \begin{pmatrix} 1&1&1\\ \epsilon&0&0\\ 0&\epsilon&0\\ 0&0&\epsilon \end{pmatrix} \end{equation} where $\epsilon$ is of the order of the machine precision, so that $1+\epsilon^2=\nobreak1$ in machine arithmetic. The CGS method proceeds as follows:
-
The first column is of length 1 in machine arithmetic, so
\begin{equation} q_1 = a_1 = \begin{pmatrix} 1\\ \epsilon\\ 0\\ 0 \end{pmatrix} . \end{equation}
-
The second column gets orthogonalized as $v\leftarrow a_2-1\cdot q_1$, giving
\begin{equation} v= \begin{pmatrix} 0\\ -\epsilon\\ \epsilon\\ 0 \end{pmatrix} , \quad\hbox{normalized:}\quad q_2 = \begin{pmatrix} 0\\ -\frac{\sqrt 2}2\\ \frac{\sqrt2}2\\ 0 \end{pmatrix} \end{equation}
-
The third column gets orthogonalized as $v\leftarrow a_3-c_1q_1-c_2q_2$, where \begin{equation} \begin{cases} c_1 = q_1^ta_3 = 1\\ c_2 = q_2^ta_3=0 \end{cases} \Rightarrow v= \begin{pmatrix} 0\\ -\epsilon\\ 0\\ \epsilon \end{pmatrix} ;\quad \hbox{normalized:}\quad q_3= \begin{pmatrix} 0\\ \frac{\sqrt2}2\\ 0\\ \frac{\sqrt2}2 \end{pmatrix} \end{equation}
-
As before, $q_1^ta_3=1$, so
\begin{equation} v\leftarrow a_3-q_1 = \begin{pmatrix} 0\\ -\epsilon\\ \epsilon\\ 0 \end{pmatrix} . \end{equation} Then, $q_2^tv=\frac{\sqrt2}2\epsilon$ (note that $q_2^ta_3=0$ before), so the second update gives
\begin{equation} v\leftarrow v- \frac{\sqrt2}2\epsilon q_2= \begin{pmatrix} 0\\ \frac\epsilon2\\ -\frac\epsilon2\\ \epsilon \end{pmatrix} ,\quad\hbox{normalized:}\quad \begin{pmatrix} 0\\ \frac{\sqrt6}6\\ -\frac{\sqrt6}6\\ 2\frac{\sqrt6}6 \end{pmatrix} \end{equation} Now all $q_i^tq_j$ are on the order of $\epsilon$ for $i\not=\nobreak j$.
13.3 The power method
crumb trail: > norms > The power method
The vector sequence \begin{equation} x_i = Ax_{i-1}, \end{equation} where $x_0$ is some starting vector, is called the \indexterm{power method} since it computes the product of subsequent matrix powers times a vector: \begin{equation} x_i = A^ix_0. \end{equation} There are cases where the relation between the $x_i$ vectors is simple. For instance, if $x_0$ is an eigenvector of $A$, we have for some scalar $\lambda$ \begin{equation} Ax_0=\lambda x_0 \qquad\hbox{and}\qquad x_i=\lambda^i x_0. \end{equation} However, for an arbitrary vector $x_0$, the sequence $\{x_i\}_i$ is likely to consist of independent vectors. Up to a point.
Exercise
Let $A$ and $x$ be the $n\times n$ matrix and dimension $n$ vector
\begin{equation}
A =
\begin{pmatrix}
1&1\\ &1&1\\ &&\ddots&\ddots\\ &&&1&1\\&&&&1
\end{pmatrix}
,\qquad
x = (0,…,0,1)^t.
\end{equation}
Show that the sequence $[x,Ax,\ldots,A^ix]$ is an independent set
for $i
Now consider the matrix $B$:
\begin{equation}
B=\left(
\begin{array}{cccc|cccc}
1&1&&\\ &\ddots&\ddots&\\ &&1&1\\ &&&1\\ \hline
&&&&1&1\\ &&&&&\ddots&\ddots\\ &&&&&&1&1\\ &&&&&&&1
\end{array}
\right),\qquad
y = (0,…,0,1)^t
\end{equation}
Show that the set $[y,By,\ldots,B^iy]$ is an independent set for
$i
While in general the vectors $x,Ax,A^2x,\ldots$ can be expected to be
independent, in computer arithmetic this story is no longer so clear.
Suppose the matrix has eigenvalues $\lambda_0>\lambda_1\geq\cdots
\lambda_{n-1}$ and corresponding eigenvectors $u_i$ so that
\begin{equation}
Au_i=\lambda_i u_i.
\end{equation}
Let the vector $x$ be written as
\begin{equation}
x=c_0u_0+\cdots +c_{n-1}u_{n-1},
\end{equation}
then
\begin{equation}
A^ix = c_0\lambda_0^iu_i+\cdots +c_{n-1}\lambda_{n-1}^iu_{n-1}.
\end{equation}
If we write this as
\begin{equation}
A^ix = \lambda_0^i\left[
c_0u_i+c_1\left(\frac{\lambda_1}{\lambda_0}\right)^i+
\cdots +c_{n-1}\left(\frac{\lambda_{n-1}}{\lambda_0}\right)^i
\right],
\end{equation}
we see that, numerically, $A^ix$ will get progressively closer
to a multiple of $u_0$, the
dominant eigenvector
.
Hence,
any calculation that uses independence of the $A^ix$ vectors is likely
to be inaccurate.
Section
5.5.9
discusses iterative methods that can be considered
as building an orthogonal basis for the span of the power method vectors.
crumb trail: > norms > Nonnegative matrices; Perron vectors
If $A$ is a nonnegative matrix, the maximal eigenvalue has the
property that its eigenvector is nonnegative: this is the the
Perron-Frobenius theorem
.
Theorem
If a nonnegative matrix $A$ is irreducible, its eigenvalues
satisfy
End of exercise
13.4 Nonnegative matrices; Perron vectors
The eigenvalue $\alpha_1$ that is largest in magnitude is real and simple:
\begin{equation} \alpha_1> |\alpha_2|\geq\cdots. \end{equation}
The corresponding eigenvector is positive.
End of theorem
The best known application of this theorem is the Googe PageRank algorithm; section 9.4 .
13.5 The Gershgorin theorem
crumb trail: > norms > The Gershgorin theorem
Finding the eigenvalues of a matrix is usually complicated. However, there are some tools to estimate eigenvalues. In this section you will see a theorem that, in some circumstances, can give useful information on eigenvalues.
Let $A$ be a square matrix, and $x,\lambda$ an eigenpair: $Ax=\lambda x$. Looking at one component, we have \begin{equation} a_{ii}x_i+\sum_{j\not=i} a_{ij}x_j=\lambda x_i. \end{equation} Taking norms: \begin{equation} (a_{ii}-\lambda) \leq \sum_{j\not=i} |a_{ij}| \left|\frac{x_j}{x_i}\right| \end{equation} Taking the value of $i$ for which $|x_i|$ is maximal, we find \begin{equation} (a_{ii}-\lambda) \leq \sum_{j\not=i} |a_{ij}|. \end{equation} This statement can be interpreted as follows:
The eigenvalue $\lambda$ is located in the circle around $a_{ii}$ with radius $\sum_{j\not=i}|a_{ij}|$.
Since we do not know for which value of $i$ $|x_i|$ is maximal, we can only say that there is some value of $i$ such that $\lambda$ lies in such a circle. This is the Gershgorin theorem .
Theorem
Let $A$ be a square matrix, and let $D_i$ be the circle with center
$a_{ii}$ and radius $\sum_{j\not=i}|a_{ij}|$, then the eigenvalues
are contained in the union of circles $\cup_i D_i$.
End of theorem
We can conclude that the eigenvalues are in the interior of these discs, if the constant vector is not an eigenvector.
13.6 Householder reflectors
crumb trail: > norms > Householder reflectors
In some contexts the question comes up how to transform one subspace into another. Householder reflectors a unit vector $u$, and let \begin{equation} H= I-2uu^t. \end{equation} For this matrix we have $Hu=-u$, and if $u\perp v$, then $Hv=v$. In other words, the subspace of multiples of $u$ is flipped, and the orthogonal subspace stays invariant.
Now for the original problem of mapping one space into another. Let the original space be spanned by a vector $x$ and the resulting by $y$, then note that \begin{equation} \begin{cases} x = (x+y)/2 + (x-y)/2\\ y = (x+y)/2 - (x-y)/2. \end{cases} \end{equation}
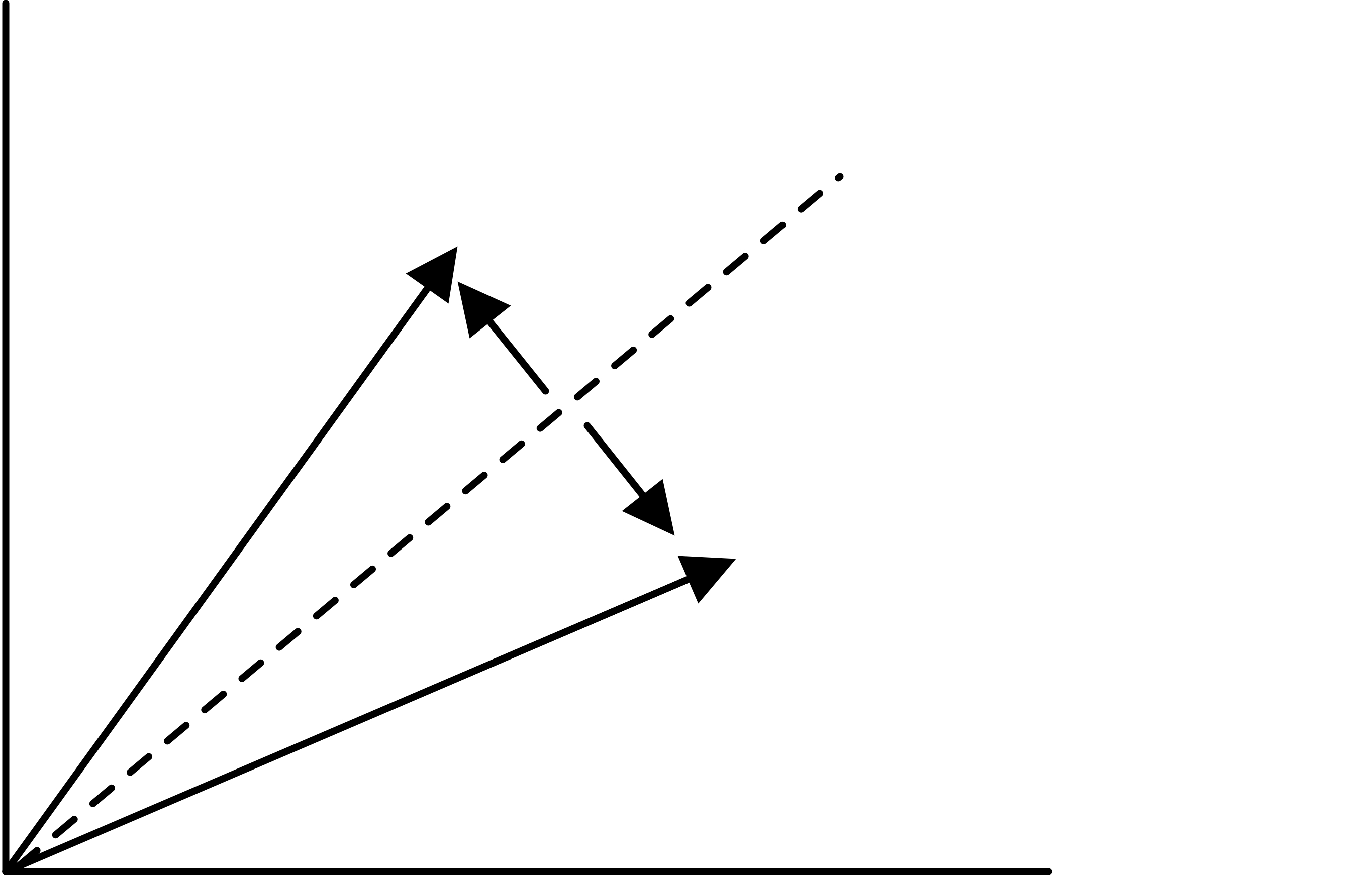
FIGURE 13.1: Householder reflector.
In other words, we can map $x$ into $y$ with the reflector based on $u=(x-y)/2$.
We can generalize Householder reflectors to a form \begin{equation} H=I-2uv^t. \end{equation} The matrices $L_i$ used in LU factorization (see section 5.3 ) can then be seen to be of the form $L_i = I-\ell_ie_i^t$ where $e_i$ has a single one in the $i$-th location, and $\ell_i$ only has nonzero below that location. That form also makes it easy to see that $L_i\inv = I+\ell_ie_i^t$: \begin{equation} (I-uv^t)(I+uv^t) = I-uv^tuv^t = 0 \end{equation} if $v^tu=0$.