25 OpenMP topic: Affinity

25.1 OpenMP thread affinity control

crumb trail: > omp-affinity > OpenMP thread affinity control

The matter of thread affinity becomes important on multi-socket nodes % ; see the example in section  25.2  .

Thread placement can be controlled with two environment variables:

• the environment variable OMP_PROC_BIND describes how threads are bound to OpenMP places ; while
• the variable OMP_PLACES describes these places in terms of the available hardware.
• When you're experimenting with these variables it is a good idea to set OMP_DISPLAY_ENV to true, so that OpenMP will print out at runtime how it has interpreted your specification. The examples in the following sections will display this output.

25.1.1 Thread binding

crumb trail: > omp-affinity > OpenMP thread affinity control > Thread binding

The variable OMP_PLACES defines a series of places to which the threads are assigned, and OMP_PROC_BIND describes how threads are tied to those places.

Typical values for OMP_PLACES are

• socket : threads are bound to a socket  , but can be moved between cores in the socket;
• core : threads are bound to a core  , but can be moved between hyperthreads in the core;
• thread : threads are bound to a specific hyper-thread  .

Values for OMP_PROC_BIND are implementation-defined, but typically:

• master : threads are bound to the same place as the master thread;
• close : subsequent thread numbers are placed close together in the defined places;
• spread : subsequent thread numbers are maxially spread over places;
• true : threads are bound to their initial placement;
• false : threads are not bound to their initial placement;

There is no runtime function for setting the binding, but the ICV bind-var can be retrieved with omp_get_proc_bind  . The binding can also be set with the \indexompclause{proc_bind} clause on the parallel directive, with values master,close,spread  .

Example: if you have two sockets and you define

OMP_PLACES=sockets

• thread 0 goes to socket 0,
• thread 1 goes to socket 1,
• thread 2 goes to socket 0 again,
• and so on.

OMP_PLACES=cores
OMP_PROC_BIND=close

• thread 0 goes to core 0, which is on socket 0,
• thread 1 goes to core 1, which is on socket 0,
• thread 2 goes to core 2, which is on socket 0,
• and so on, until thread 7 goes to core 7 on socket 0, and
• thread 8 goes to core 8, which is on socket 1,
• et cetera.

OMP_PLACES=cores
OMP_PROC_BIND=spread

• thread 0 goes to core 0, which is on socket 0,
• thread 1 goes to core 8, which is on socket 1,
• thread 2 goes to core 1, which is on socket 0,
• thread 3 goes to core 9, which is on socket 1,
• and so on, until thread 14 goes to core 7 on socket 0, and
• thread 15 goes to core 15, which is on socket 1.

So you see that OMP_PLACES=cores and OMP_PROC_BIND=spread very similar to OMP_PLACES=sockets  . The difference is that the latter choice does not bind a thread to a specific core, so the operating system can move threads about, and it can put more than one thread on the same core, even if there is another core still unused.

The value OMP_PROC_BIND=master puts the threads in the same place as the master of the team. This is convenient if you create teams recursively. In that case you would use the \indexclause{proc\_bind} clause rather than the environment variable, set to spread for the initial team, and to master for the recursively created team.

25.1.2 Effects of thread binding

crumb trail: > omp-affinity > OpenMP thread affinity control > Effects of thread binding

Let's consider two example program. First we consider the program for computing $\pi$, which is purely compute-bound.

\toprule \#threads	close/cores	spread/sockets	spread/cores
\midrule 1	0.359	0.354	0.353
2	0.177	0.177	0.177
4	0.088	0.088	0.088
6	0.059	0.059	0.059
8	0.044	0.044	0.044
12	0.029	0.045	0.029
16	0.022	0.050	0.022
\bottomrule

We see pretty much perfect speedup for the OMP_PLACES=cores strategy; with OMP_PLACES=sockets we probably get occasional collisions where two threads wind up on the same core.

Next we take a program for computing the time evolution of the heat equation : \begin{equation} t=0,1,2,…\colon \forall_i\colon x^{(t+1)}_i = 2x^{(t)}_i-x^{(t)}_{i-1}-x^{(t)}_{i+1} \end{equation} This is a bandwidth-bound operation because the amount of computation per data item is low.

\toprule \#threads	close/cores	spread/sockets	spread/cores
\midrule 1	2.88	2.89	2.88
2	1.71	1.41	1.42
4	1.11	0.74	0.74
6	1.09	0.57	0.57
8	1.12	0.57	0.53
12	0.72	0.53	0.52
16	0.52	0.61	0.53
\bottomrule

Again we see that OMP_PLACES=sockets gives worse performance for high core counts, probably because of threads winding up on the same core. The thing to observe in this example is that with 6 or 8 cores the OMP_PROC_BIND=spread strategy gives twice the performance of OMP_PROC_BIND=close  .

The reason for this is that a single socket does not have enough bandwidth for all eight cores on the socket. Therefore, dividing the eight threads over two sockets gives each thread a higher available bandwidth than putting all threads on one socket.

25.1.3 Place definition

crumb trail: > omp-affinity > OpenMP thread affinity control > Place definition

There are three predefined values for the OMP_PLACES variable: sockets, cores, threads  . You have already seen the first two; the threads value becomes relevant on processors that have hardware threads. In that case, OMP_PLACES=cores does not tie a thread to a specific hardware thread, leading again to possible collisions as in the above example. Setting OMP_PLACES=threads ties each OpenMP thread to a specific hardware thread.

There is also a very general syntax for defining places that uses a

  location:number:stride

• OMP_PLACES="{0:8:1},{8:8:1}"
  

  is equivalent to sockets on a two-socket design with eight cores per socket: it defines two places, each having eight consecutive cores. The threads are then places alternating between the two places, but not further specified inside the place.
• The setting cores is equivalent to

  OMP_PLACES="{0},{1},{2},...,{15}"
  

• On a four-socket design, the specification

  OMP_PLACES="{0:4:8}:4:1"
  

  states that the place 0,8,16,24 needs to be repeated four times, with a stride of one. In other words, thread 0 winds up on core 0 of some socket, the thread 1 winds up on core 1 of some socket, et cetera.

25.1.4 Binding possibilities

crumb trail: > omp-affinity > OpenMP thread affinity control > Binding possibilities

Values for OMP_PROC_BIND are: false, true, master, close, spread  .

• false: set no binding
• true: lock threads to a core
• master: collocate threads with the master thread
• close: place threads close to the master in the places list
• spread: spread out threads as much as possible

This effect can be made local by giving the \indexclause{proc\_bind} clause in the parallel directive.

A safe default setting is

export OMP_PROC_BIND=true

Good examples of thread placement on the Intel Knight's Landing :

https://software.intel.com/en-us/articles/process-and-thread-affinity-for-intel-xeon-phi-processors-x200

As an example, consider a code where two threads write to a shared location.

// sharing.c
#pragma omp parallel
  { // not a parallel for: just a bunch of reps
    for (int j = 0; j < reps; j++) {
#pragma omp for schedule(static,1)
      for (int i = 0; i < N; i++){
#pragma omp atomic
	a++;  
      }


      

    }
  }

OMP_NUM_THREADS=2 OMP_PLACES=cores OMP_PROC_BIND=close ./sharing
run time = 4752.231836usec
sum = 80000000.0

OMP_PLACES=threads OMP_PROC_BIND=close ./sharing
run time = 941.970110usec
sum = 80000000.0

OMP_NUM_THREADS=1 OMP_PLACES=cores OMP_PROC_BIND=close ./sharing
run time = 806.669950usec
sum = 80000000.0

25.2 First-touch

crumb trail: > omp-affinity > First-touch

The affinity issue shows up in the first-touch phenomemon.

A little background knowledge. Memory is organized in memory page s, and what we think of as `addresses' really virtual address es, mapped to physical address es, through a page table  .

This means that data in your program can be anywhere in physical memory. In particular, on a dual socket node, the memory can be mapped to either of the sockets.

The next thing to know is that memory allocated with malloc and like routines is not immediately mapped; that only happens when data is written to it. In light of this, consider the following OpenMP code:

double *x = (double*) malloc(N*sizeof(double));

for (i=0; i<N; i++)
  x[i] = 0;

#pragma omp parallel for
for (i=0; i<N; i++)
  .... something with x[i] ...

Let's consider an example. We make the initialization parallel subject to an option:

// heat.c
#pragma omp parallel if (init>0)
  {
#pragma omp for
    for (int i=0; i<N; i++)
      y[i] = x[i] = 0.;
    x[0] = 0; x[N-1] = 1.;
  }

If the initialization is not parallel, the array will be mapped to the socket of the master thread; if it is parallel, it may be mapped to different sockets, depending on where the threads run.

As a simple application we run a heat equation, which is parallel, though not embarassingly so:

for (int it=0; it<1000; it++) {
#pragma omp parallel for
  for (int i=1; i<N-1; i++)
    y[i] = ( x[i-1]+x[i]+x[i+1] )/3.;
#pragma omp parallel for
  for (int i=1; i<N-1; i++)
    x[i] = y[i];
}

On the TACC Frontera machine, with dual 28-core Intel Cascade Lake processors, we use the following settings:

export OMP_PLACES=cores
export OMP_PROC_BIND=close
# no parallel initialization
make heat && OMP_NUM_THREADS=56 ./heat
# yes parallel initialization
make heat && OMP_NUM_THREADS=56 ./heat 1

This gives us a remarkable difference in runtime:

• Sequential init: avg=2.089, stddev=0.1083
• Parallel init: avg=1.006, stddev=0.0216

Exercise How do the OpenMP dynamic schedules relate to this issue?
End of exercise

25.2.1 C++

crumb trail: > omp-affinity > First-touch > C++

The problem with realizing first-touch in C++ %

is that std::vector fills its allocation with default values. This is known as `value-initialization', and it makes

vector<double> x(N);

Here is a solution. C++ note Default initialization is a problem. We make a template for uninitialized types:

// heatalloc.cxx
template<typename T>
struct uninitialized {
  uninitialized() {};
  T val;
  constexpr operator T() const {return val;};
  T operator=( const T&& v ) { val = v; return val; };
};

so that we can create vectors that behave normally:

vector<uninitialized<double>> x(N),y(N);




#pragma omp parallel for
for (int i=0; i<N; i++)
  y[i] = x[i] = 0.;
x[0] = 0; x[N-1] = 1.;

Running the code with the regular definition of a vector, and the above modification, reproduces the runtimes of the C variant above.

Another option is to wrap memory allocated with new in a unique_ptr :

// heatptr.cxx
unique_ptr<double[]> x( new double[N] );
unique_ptr<double[]> y( new double[N] );




#pragma omp parallel for
for (int i=0; i<N; i++) {
  y[i] = x[i] = 0.;
}
x[0] = 0; x[N-1] = 1.;

Note that this gives fairly elegant code, since square bracket indexing is overloaded for unique_ptr . The only disadvantage is that we can not query the size of these arrays. Or do bound checking with at  , but in high performance contexts that is usually not appropriate anyway.

25.2.2 Remarks

crumb trail: > omp-affinity > First-touch > Remarks

You could move pages with move_pages  .

By regarding affinity, in effect you are adopting an SPMD style of programming. You could make this explicit by having each thread allocate its part of the arrays separately, and storing a private pointer as threadprivate   [Liu:2003:OMP-SPMD]  . However, this makes it impossible for threads to access each other's parts of the distributed array, so this is only suitable for total data parallel or embarrassingly parallel applications.

25.3 Affinity control outside OpenMP

crumb trail: > omp-affinity > Affinity control outside OpenMP

There are various utilities to control process and thread placement.

Process placement can be controlled on the Operating system level by \indextermttdef{numactl}

on Linux (also taskset  ); Windows start/affinity  .

Corresponding system calls: pbing on Solaris, sched_setaffinity on Linux, SetThreadAffinityMask on Windows.

Corresponding environment variables: SUNW_MP_PROCBIND on Solaris, KMP_AFFINITY on Intel.

The Intel compiler has an environment variable for affinity control:

export KMP_AFFINITY=verbose,scatter

For gcc :

export GOMP_CPU_AFFINITY=0,8,1,9

For the Sun compiler :

SUNW_MP_PROCBIND

25.4 Tests

crumb trail: > omp-affinity > Tests

We take a simple loop and consider the influence of binding parameters.

// speedup.c
#pragma omp parallel for
      for (int ip=0; ip<N; ip++) {
        for (int jp=0; jp<M; jp++) {
          double f = sin( values[ip] );
          values[ip] = f;
        }
      }   

25.4.1 Lonestar 6

crumb trail: > omp-affinity > Tests > Lonestar 6

Lonestar 6, dual socket AMD Milan  , total 112 cores: figure  25.1  .

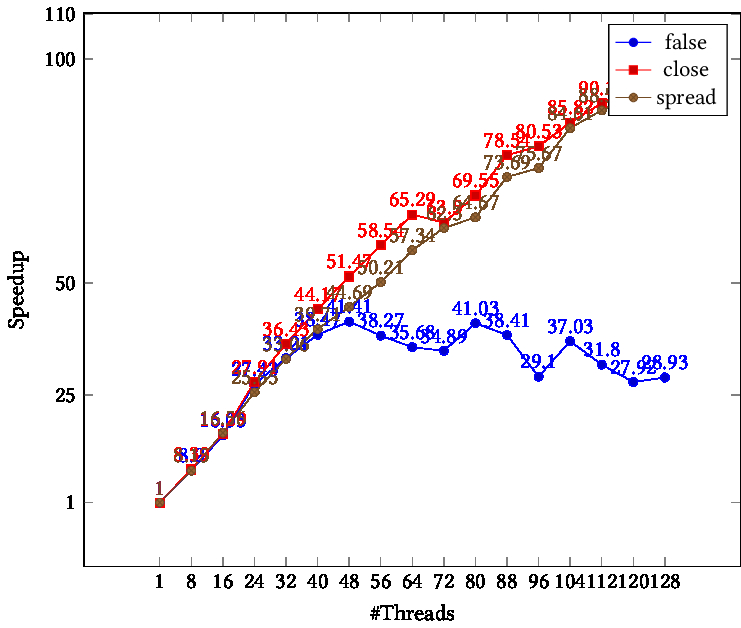
TIKZPICTURE 25.1: Speedup as function of thread count, Lonestar 6 cluster, different binding parameters

25.4.2 Frontera

crumb trail: > omp-affinity > Tests > Frontera

Intel Cascade Lake  , dual socket, 56 cores total; figure  25.2  .

For all core counts to half the total, performance for all binding strategies seems equal. After that , close and spread perform equally, but the speedup for the false value gives erratic numbers.

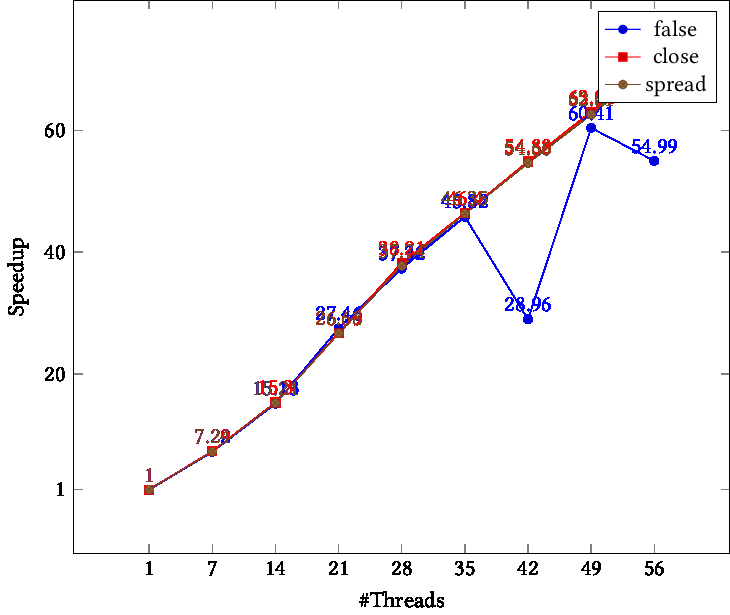
TIKZPICTURE 25.2: Speedup as function of thread count, Frontera cluster, different binding parameters

25.4.3 Stampede2 skylake

crumb trail: > omp-affinity > Tests > Stampede2 skylake

Dual 24-core Intel Skylake ; figure  25.3  .

We see that close binding gives worse performance than spread  . Setting binding to false only gives bad performance for large core counts.

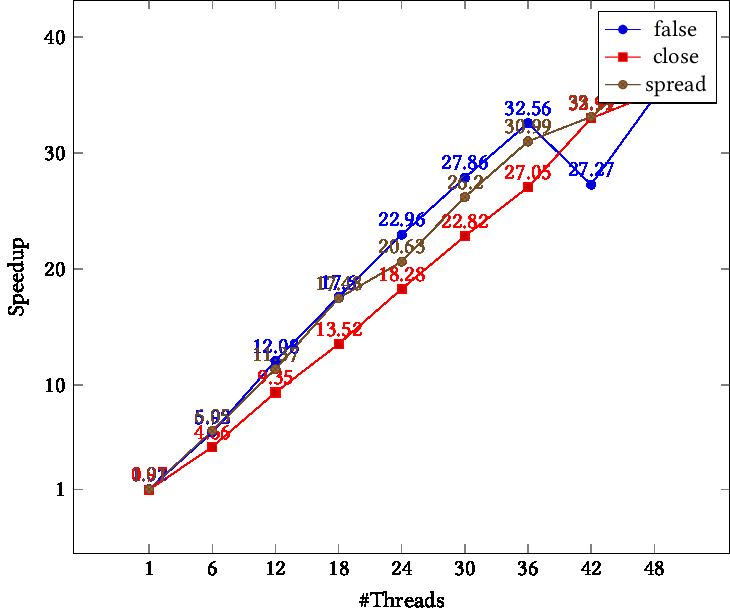
TIKZPICTURE 25.3: Speedup as function of thread count, Stampede2 skylake cluster, different binding parameters

25.4.4 Stampede2 Knights Landing

crumb trail: > omp-affinity > Tests > Stampede2 Knights Landing

We test on a single socket 68-core processor: the Intel Knights Landing  .

Since this is a single socket design, we don't distinguish between the close and spread binding. However, the binding value of true shows good speedup -- in fact beyond the core count -- while false gives worse performance than in other architectures.

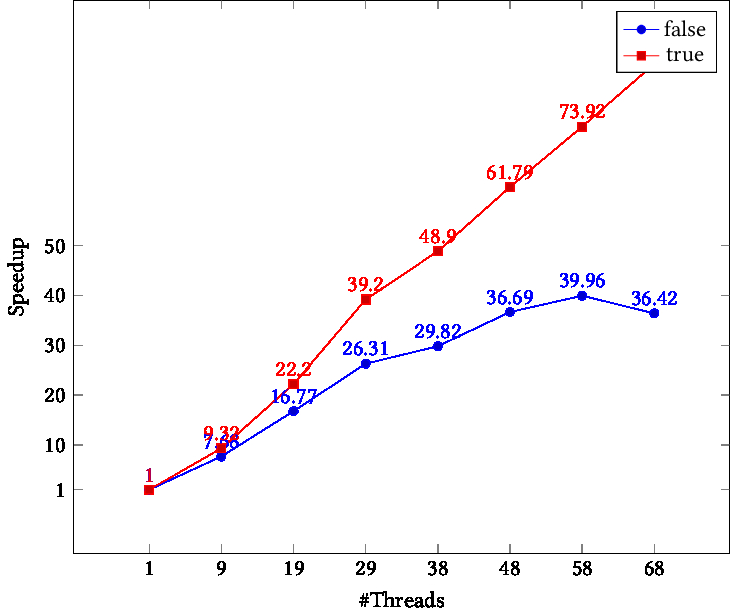
TIKZPICTURE 25.4: Speedup as function of thread count, Stampede2 Knights Landing cluster, different binding parameters

25.4.5 Longhorn

crumb trail: > omp-affinity > Tests > Longhorn

Dual 20-core IBM Power9  , 4 hyperthreads; 25.5

Unlike the Intel processors, here we use the hyperthreads. Figure  25.5 shows dip in the speedup at 40 threads. For higher thread counts the speedup increases to well beyond the physical core count of $40$.

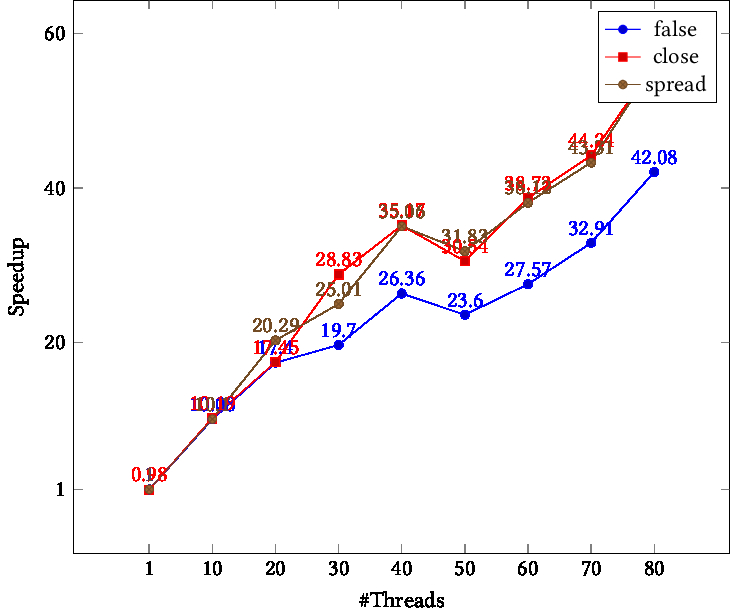
TIKZPICTURE 25.5: Speedup as function of thread count, Longhorn cluster, different binding parameters