33 Grid support

PETSc's DM objects raise the abstraction level from the linear algebra problem to the physics problem: they allow for a more direct expression of operators in terms of their domain of definition. In this section we look at the DMDA `distributed array' objects, which correspond to problems defined on Cartesian grids. Distributed arrays make it easier to construct the coefficient matrix of an operator that is defined as a stencil on a 1/2/3-dimensional Cartesian grid  .

The main creation routine exists in three variants that mostly differ their number of parameters. For instance, DMDACreate2d has parameters along the \clstinline{x,y} axes. However, DMDACreate1d has no parameter for the stencil type, since in 1D those are all the same, or for the process distribution.

33.1 Grid definition

crumb trail: > petsc-dmda > Grid definition

A two-dimensional grid is created with DMDACreate2d

DMDACreate2d( communicator,
  x_boundary,y_boundary,
  stenciltype,
  gridx,gridy, procx,procy, dof,width, 
  partitionx,partitiony, 
  grid);

• Boundary type is a value of type DMBoundaryType  . Values are:
  • DM_BOUNDARY_NONE
  • DM_BOUNDARY_GHOSTED  ,
  • DM_BOUNDARY_PERIODIC  ,

• 

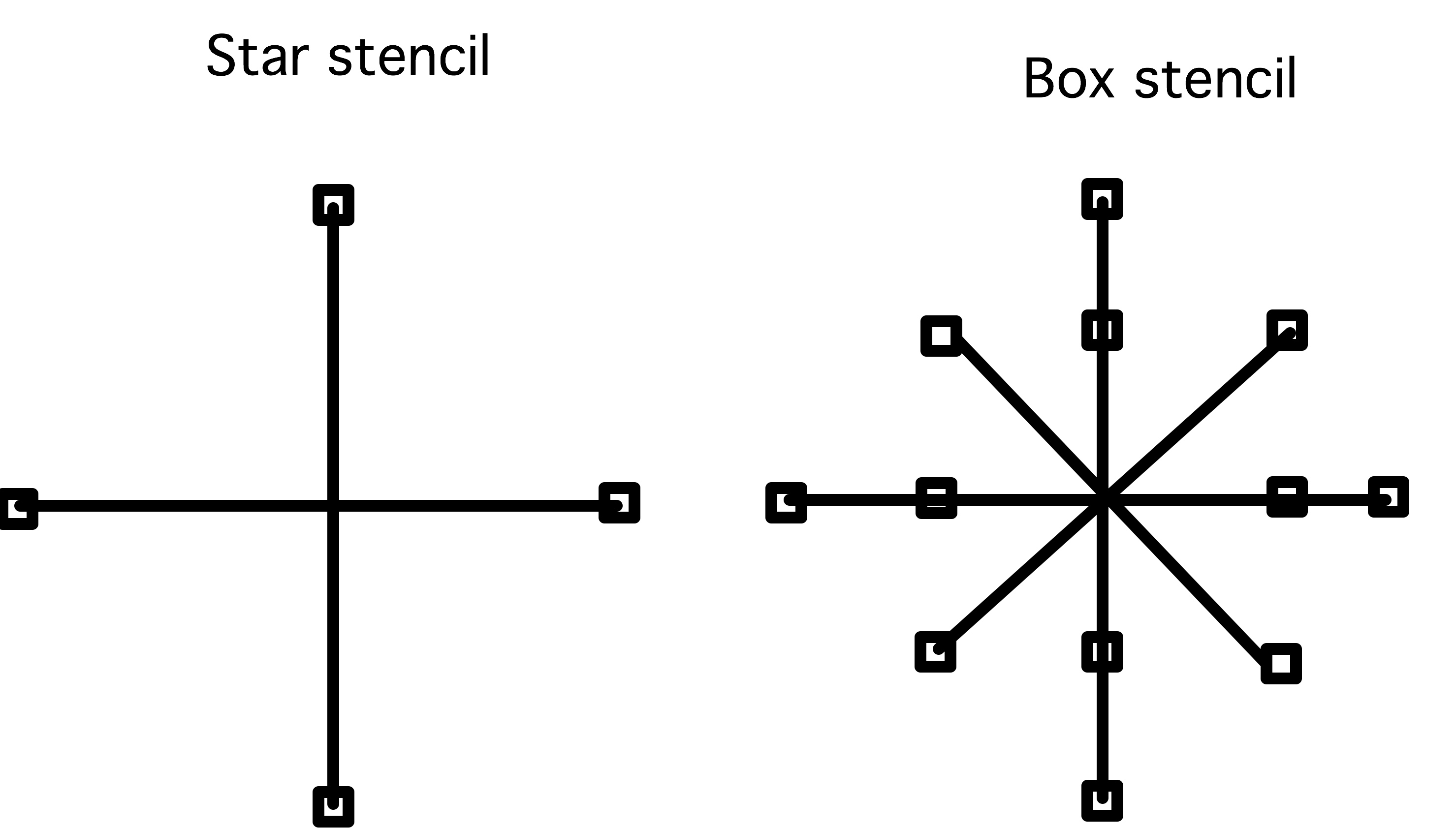
  FIGURE 33.1: Star and box stencils

  The stencil type is of type DMStencilType  , with values

  • DMDA_STENCIL_BOX  ,
  • DMDA_STENCIL_STAR  .
  (See figure  33.1  .)
• The gridx,gridy values are the global grid size. This can be set with commandline options da_grid_x /y/z .
• The procx,procy variables are an explicit specification of the processor grid. Failing this specification, PETSc will try to find a distribution similar to the domain grid.
• dof indicates the number of `degrees of freedom', where 1 corresponds to a scalar problem.
• width indicates the extent of the stencil: 1 for a 5-point stencil or more general a 2nd order stencil for 2nd order PDEs  , 2 for 2nd order discretizations of a 4th order PDE  , et cetera.
• partitionx,partitiony are arrays giving explicit partitionings of the grid over the processors, or PETSC_NULL for default distributions.

\csnippetwithoutput{dm2dcreate}{examples/petsc/c}{dmcreate}

After you define a DM object, each process has a contiguous subdomain out of the total grid. You can query its size and location with DMDAGetCorners  , or query that and all other information with DMDAGetLocalInfo  , which returns an DMDALocalInfo structure.

(A DMDALocalInfo struct is the same for 1/2/3 dimensions, so certain fields may not be applicable to your specific PDE  .)

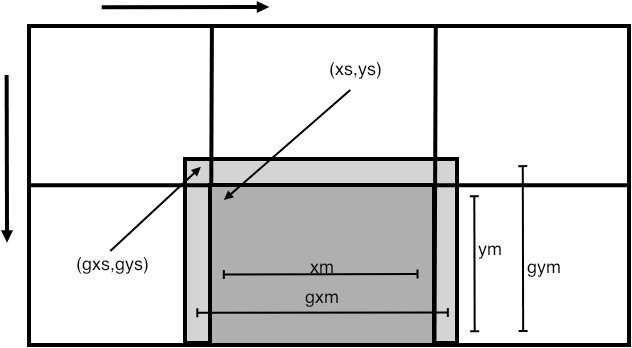
FIGURE 33.2: Illustration of various fields of the DMDALocalInfo structure

33.1.1 Associated vectors

crumb trail: > petsc-dmda > Grid definition > Associated vectors

Using the fields in this structure, each process can now iterate over its own subdomain. For instance, the `top left' corner of the owned subdomain is at xs,ys and the number of points is xm,ym (see figure  33.2  ), so we can iterate over the subdomain as:

for (int j=info.ys; j<info.ys+info.ym; j++) {
  for (int i=info.xs; i<info.xs+info.xm; i++) {
    // actions on point i,j
  }
}

On each point of the domain, we describe the stencil at that point. First of all, we now have the information to compute the $x,y$ coordinates of the domain points:

PetscReal **xyarray;
PetscCall( DMDAVecGetArray(grid,xy,&xyarray) );
for (int j=info.ys; j<info.ys+info.ym; j++) {
  for (int i=info.xs; i<info.xs+info.xm; i++) {
	PetscReal x = i*hx, y = j*hy;
	xyarray[j][i] = x*y;
  }
}
PetscCall( DMDAVecRestoreArray(grid,xy,&xyarray) );

In some circumstances, we want to perform stencil operations on the vector of a DMDA grid. This requires having the halo region  . Above, you already saw the gxs,gxm and other quantities relating to the halo of each process' subdomain.

What we need is a way to make vectors that contain these halo points.

• You can make a traditonal vector corresponding to a grid with DMCreateGlobalVector ; if you need this vector only for a short while, use DMGetGlobalVector and DMRestoreGlobalVector  .
• You can make a vector including halo points with DMCreateLocalVector ; if you need this vector only for a short while, use DMGetLocalVector and DMRestoreLocalVector  .
• If you have a `global' vector, you can made the corresponding `local' vector, filling in its halo points, with DMGlobalToLocal ; after operating on a local vector, you can copy its non-halo part back to a global vector with DMLocalToGlobal  .

Here we set up a local vector for operations:

Vec ghostvector;
PetscCall( DMGetLocalVector(grid,&ghostvector) );
PetscCall( DMGlobalToLocal(grid,xy,INSERT_VALUES,ghostvector) );
PetscReal **xyarray,**gh;
PetscCall( DMDAVecGetArray(grid,xy,&xyarray) );
PetscCall( DMDAVecGetArray(grid,ghostvector,&gh) );
// computation on the arrays
PetscCall( DMDAVecRestoreArray(grid,xy,&xyarray) );
PetscCall( DMDAVecRestoreArray(grid,ghostvector,&gh) );
PetscCall( DMLocalToGlobal(grid,ghostvector,INSERT_VALUES,xy) );
PetscCall( DMRestoreLocalVector(grid,&ghostvector) );

The actual operations involve some tests for the actual presence of the halo:

for (int j=info.ys; j<info.ys+info.ym; j++) {
  for (int i=info.xs; i<info.xs+info.xm; i++) {
	if (info.gxs<info.xs && info.gys<info.ys)
	  if (i-1>=info.gxs && i+1<=info.gxs+info.gxm &&
	      j-1>=info.gys && j+1<=info.gys+info.gym )
	    xyarray[j][i] =
	      ( gh[j-1][i] + gh[j][i-1] + gh[j][i+1] + gh[j+1][i] )
	      /4.;

33.1.2 Associated matrix

crumb trail: > petsc-dmda > Grid definition > Associated matrix

We construct a matrix on a DMDA by constructing a stencil on every $(i,j)$ coordinate on a process:

for (int j=info.ys; j<info.ys+info.ym; j++) {
  for (int i=info.xs; i<info.xs+info.xm; i++) {
    PetscReal x = i*hx, y = j*hy;
    ...
    // set the row, col, v values
    ierr = MatSetValuesStencil(A,1,&row,ncols,col,v,INSERT_VALUES);CHKERRQ(ierr);
  }
}

Each matrix element row,col is a combination of two MatStencil objects. Technically, this is a struct with members i,j,k,s for the domain coordinates and the number of the field.

MatStencil  row;
row.i = i; row.j = j; 

MatStencil col[5];
PetscScalar v[5];
PetscInt    ncols = 0;
/**** diagonal element ****/
col[ncols].i = i; col[ncols].j = j;
v[ncols++] = 4.;
/**** off diagonal elements ****/
 ....

The other `legs' of the stencil need to be set conditionally: the connection to $(i-1,j)$ is missing on the top row of the domain, and the connection to $(i,j-1)$ is missing on the left column. In all:

// grid2d.c
for (int j=info.ys; j<info.ys+info.ym; j++) {
  for (int i=info.xs; i<info.xs+info.xm; i++) {
    MatStencil  row,col[5];
    PetscScalar v[5];
    PetscInt    ncols = 0;
    row.j        = j; row.i = i;
    /**** local connection: diagonal element ****/
    col[ncols].j = j; col[ncols].i = i; v[ncols++] = 4.;
    /* boundaries: top and bottom row */
    if (i>0)         {col[ncols].j = j;   col[ncols].i = i-1; v[ncols++] = -1.;}
    if (i<info.mx-1) {col[ncols].j = j;   col[ncols].i = i+1; v[ncols++] = -1.;}
    /* boundary left and right */
    if (j>0)         {col[ncols].j = j-1; col[ncols].i = i;   v[ncols++] = -1.;}
    if (j<info.my-1) {col[ncols].j = j+1; col[ncols].i = i;   v[ncols++] = -1.;}




    PetscCall( MatSetValuesStencil(A,1,&row,ncols,col,v,INSERT_VALUES) );
  }
}

33.2 Constructing a vector on a grid

crumb trail: > petsc-dmda > Constructing a vector on a grid

A DMDA object is a description of a grid, so we now need to concern how to construct a linear system defined on that grid.

We start with vectors: we need a solution vector and a right-hand side. Here we have two options:

1. we can build a vector from scratch that has the right structure; or
2. we can use the fact that a grid object has a vector that can be extracted.

33.2.1 Create confirming vector

crumb trail: > petsc-dmda > Constructing a vector on a grid > Create confirming vector

If we create a vector with VecCreate and VecSetSizes  , it is easy to get the global size right, but the default partitioning will probably not be conformal to the grid distribution. Also, getting the indexing scheme right is not trivial.

First of all, the local size needs to be set explicitly, using information from the DMDALocalInfo object:

Vec xy;
PetscCall( VecCreate(comm,&xy) );
PetscCall( VecSetType(xy,VECMPI) );
PetscInt nlocal = info.xm*info.ym, nglobal = info.mx*info.my;
PetscCall( VecSetSizes(xy,nlocal,nglobal) );

After this, you don't use VecSetValues  , but set elements directly in the raw array, obtained by DMDAVecGetArray :

PetscReal **xyarray;
PetscCall( DMDAVecGetArray(grid,xy,&xyarray) );
for (int j=info.ys; j<info.ys+info.ym; j++) {
  for (int i=info.xs; i<info.xs+info.xm; i++) {
	PetscReal x = i*hx, y = j*hy;
	xyarray[j][i] = x*y;
  }
}
PetscCall( DMDAVecRestoreArray(grid,xy,&xyarray) );

33.2.2 Extract vector from DMDA

crumb trail: > petsc-dmda > Constructing a vector on a grid > Extract vector from DMDA

33.2.3 Refinement

crumb trail: > petsc-dmda > Constructing a vector on a grid > Refinement

The routine DMDASetRefinementFactor can be activated with the options da_refine or separately da_refine_x /y/z for the directions.

33.3 Vectors of a distributed array

crumb trail: > petsc-dmda > Vectors of a distributed array

A distributed array is similar to a distributed vector, so there are routines of extracting the values of the array in the form of a vector. This can be done in two ways: of ways. (The routines here actually pertain to the more general DM `Data Management' object, but we will for now discuss them in the context of DMDA  .)

1. You can create a `global' vector, defined on the same communicator as the array, and which is disjointly partitioned in the same manner. This is done with DMCreateGlobalVector :

   PetscErrorCode DMCreateGlobalVector(DM dm,Vec *vec)    
   

2. You can create a `local' vector, which is sequential and defined on PETSC_COMM_SELF  , that has not only the points local to the process, but also the `halo' region with the extent specified in the definition of the \clstinline{DMDACreate} call. For this, use DMCreateLocalVector :

   PetscErrorCode DMCreateLocalVector(DM dm,Vec *vec)
   

Values can be moved between local and global vectors by:

• DMGlobalToLocal : this establishes a local vector, including ghost/halo points from a disjointly distributed global vector. (For overlapping communication and computation, use DMGlobalToLocalBegin and DMGlobalToLocalEnd  .)
• DMLocalToGlobal : this copies the disjoint parts of a local vector back into a global vector. (For overlapping communication and computation use DMLocalToGlobalBegin and DMLocalToGlobalEnd  .)

33.4 Matrices of a distributed array

crumb trail: > petsc-dmda > Matrices of a distributed array

Once you have a grid, can create its associated matrix:

DMSetUp(grid);
DMCreateMatrix(grid,&A)

With this subdomain information you can then start to create the coefficient matrix:

DM grid;
PetscInt i_first,j_first,i_local,j_local;
DMDAGetCorners(grid,&i_first,&j_first,NULL,&i_local,&j_local,NULL);
for ( PetscInt i_index=i_first; i_index<i_first+i_local; i_index++) {
  for ( PetscInt j_index=j_first; j_index<j_first+j_local; j_index++) {
  // construct coefficients for domain point (i_index,j_index)
  }
}

For a simple example, consider 1-dimensional smoothing. From DMDAGetCorners we need only the parameters in $i$-direction: \cverbatimsnippet[examples/petsc/c/grid1d.c]{dmda1corners}

We then use a single loop to set elements for the local range in $i$-direction: \cverbatimsnippet[examples/petsc/c/grid1d.c]{dmda1stencil}